17.11.2022 г.

Лекция "Производная и ее применение"

Законспектируйте лекцию, разберите все примеры.

Рассмотрим функцию . Выберем некоторое фиксированное значение аргумента , при котором данная функция определена. Пусть функция определена и в некоторой окрестности точки . Теперь выберем какую-то произвольную точку из этой окрестности точки . Найдем разность второго и первого значений аргумента: . Обозначим эту разность (читается "дельта икс"). Значение функции в точке равно . Значение функции в точке равно . Составим разность . Эта разность обозначается (читается "дельта эф").

Определение

Пусть функция определена в некоторой окрестности точки , а точка принадлежит этой окрестности. Тогда разность называется приращением аргумента в точке , а разность называется приращением функции в точке , соответствующим приращению аргумента .

Поскольку , то . Говорят, что значение аргумента получило приращение .

Значение функции в точке равно . Значение функции в точке равно . Учитывая. что , получим .

Итак,

Замечания

1) Приращение не значит увеличение. Значения и могут принимать как положительные, так и отрицательные значения.

2) Приращение функции при фиксированном значении аргумента зависит от приращения аргумента , то есть является функцией от переменной .

Приведем графическую иллюстрацию рассмотренных понятий.

Пример 1. Сторона квадрата равна . Найдите приращение его периметра, если сторону увеличили на .

Решение

Периметр квадрата есть функция его стороны . .

По условию , .

Следовательно, , , .

Ответ: .

Пример 2. Найдите приращение функции в точке , соответствующее приращению аргумента .

Решение

, .

Ответ: .

Пример 3. Найдите приращение аргумента и приращение функции в точке , если , , .

Решение

Ответ: .

Пример 4. Выразите приращение функции в точке через и .

Решение

, .

Ответ: .

watch?v=vSNGYnE_zfU

ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ.

МЕХАНИЧЕСКИЙ, ГЕОМЕТРИЧЕСКИЙ

И ЭКОНОМИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Пусть функция определена на промежутке . Возьмем произвольную точку . Дадим значению приращение , тогда функция получит приращение .

Определение. Производной функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

Производная функции имеет несколько обозначений: , , , .

Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, .

Процесс нахождения производной функции называется дифференцированием этой функции.

Если функция в точке имеет конечную производную, то функция называется дифференцируемой в этой точке.

Функция, дифференцируемая во всех точках промежутка , называется дифференцируемой на этом промежутке.

Если функция дифференцируема на промежутке , то каждому из этого промежутка поставлено в соответствие, кроме значения функции , некоторое число, равное производной функции в этой точке , т.е. на промежутке возникает, кроме , еще одна функция , которая называется производной функцией от данной функции или просто производной от этой функции: .

Из задачи о скорости прямолинейного движения следует механический смысл производной: производная пути по времени есть скорость точки в момент : .

Из задачи о касательной к графику функции вытекает геометрический смысл производной: производная есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой в точке , т.е. .

Из задачи о производительности труда следует, что производная объема произведенной продукции по времени есть производительность труда в момент .

Непрерывность функции

Основные определения

Пусть f(x) определена в некоторой окрестности точки x0 . ОПРЕДЕЛЕНИЕ 1. Функция f(x) называется непрерывной в точке x0 если справедливо равенство

ОПРЕДЕЛЕНИЕ. Функция f(x) называется непрерывной на интервале (a; b) если она непрерывна в каждой точке этого интервала. Функция f(x) называется непрерывной на отрезке [a; b] если она непрерывна на интервале (a; b) и имеет одностороннюю непрерывность в граничных точках (т.е. непрерывна в точке a справа, в точке b – слева).

Правила вычисления производных

Постоянный множитель c можно выносить за знак производной:

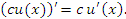
Правило 1 непосредственно вытекает из определения производной функции и свойства пределов функций, согласно которому постоянный множитель можно выносить за знак предела.

Если существуют производные 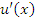и 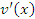, то производная от суммы (разности) функци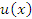й и 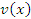равна сумме (разности) производных: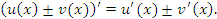

Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов.

Если существуют производные 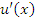и 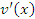, то выполняются следующие правила дифференцирования произведения функций и частного от их деления: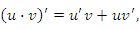

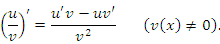
Пройдите по ссылке и посмотрите следующие видеоуроки

1. Производная степенной функции

https://www.berdov.com/docs/fluxion/proizvodnaja-stepennojj-funkcii/

2. Производная суммы и разности, производная произведения и частного

https://www.youtube.com/watch?v=ArR5jIHNCr0

Тема1: Радианная мера угла

10.02.2022 г.

Тема: "Векторы и линейные операции над ними"

Домашнее задание

07.02.2022 г.

Тема: "Тела вращения"

Пройдите по ссылке и сделайте конспект

https://docs.google.com/presentation/d/14QxoeRnmcQiCOkKlEexNOzF3KPW1q_Mc/edit?usp=sharing&ouid=112134011332415081207&rtpof=true&sd=true

02.11.2021 г.

Тема: "Аксиомы стереометрии"

Пройдите по ссылке и сделайте конспект в тетради

https://docs.google.com/document/d/1ZvRcpdeljemnb_0eyF1equI_FP2nZOUD/edit?usp=sharing&ouid=101701489737989990936&rtpof=true&sd=true

Ссылка на учебник по геометрии

https://uchebnik-skachatj-besplatno.com/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F/%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F%20%D0%A3%D1%87%D0%B5%D0%B1%D0%BD%D0%B8%D0%BA%2010-11%D0%BA%D0%BB%D0%B0%D1%81%D1%81%20%D0%90%D1%82%D0%B0%D0%BD%D0%B0%D1%81%D1%8F%D0%BD/index.html#prettyPhoto

5.11.2021 г.

Тема: "Понятие многогранника. Пирамида"
Пройдите по ссылке и сделайте конспект в тетради

https://docs.google.com/document/d/1_En4s2H16JwGG4wVTmCgDlIsrWKW06U-/edit?usp=sharing&ouid=112134011332415081207&rtpof=true&sd=true

Просмотрите видеоурок

https://www.youtube.com/watch?v=Olyy0IDNmQo

24.02.2020г.

Самостоятельная работа на 45 минут. Отправляем на почту

umadgu@mail.ru до 14.00 24.02.2021г.

27/11/2020

Домашнее задание.

Отправляем на почту umadgu@mail.ru до 12.00 28/11/2020

23/11/2020

Просмотрите следующие видеоуроки:

1. Производная суммы и разности, производная произведения и частного

https://www.youtube.com/watch?v=ArR5jIHNCr0

2. Производная сложной функции

https://yandex.ru/efir?stream_id=44d6ced5c445e4509e8aa95eb51f5aee

Жду ваше выполненное домашнее задание

22/09/2021

Здравствуйте! Самостоятельная работа на 45 минут!

Позже 13.40 работа не принимается!!!!!!! Не забудьте указать фамилию, имя и группу на своей работе!!!! Удачи всем!!!

Чтобы рассмотреть самостоятельно тему "Тригонометрические функции и их графики", вы можете пройти по ссылке https://drive.google.com/file/d/1QhW2suVqaTjuviEs0pOajFWg8Q2y7vmJ/view?usp=sharing.

А также в учебнике стр.14-19.

Домашнее задание на 05.09.2020 г.

Выполнить № 1(а,б), №2 (а,б)

и №3 (завершить)

2020-2021 учебный год

Задание на 19.06.2020 г.

Выполните контрольную работу, результаты жду до 18.00 (пятницы). Позже не принимаю!

Задание на 16.06.2020 г.

Домашнее задание:

1) Перейти по ссылке. Выписать все формулы, таблицы в тетрадь. На экзамене вам пригодятся эти записи. В тестах будут такие задания, как: Какая из формул правильная? И по вашим записям можно будет легко определить правильную формулу.

https://drive.google.com/file/d/1vl1WxY7VArWbDtFKZLhxLjCa7Z5IrGm9/view?usp=sharing

2) Вычислить:

Задание на 15.06.2020 г.

Задание на 11.06.2020 г.

Выполнить номера №485, №486,№487

Задание на 09.06.2020 г.

Выполнить номера №483, №484

Задание на 08.06.2020 г.

Тема: Логарифмы и их свойства

Ребята, обязательно выпишите все формулы в конец тетради, выучите все свойства логарифма и основное логарифмическое тождество. На экзамене вам пригодится знание формул.

https://drive.google.com/file/d/1_nFKXHyqrYfGSk7AoypOBqFpzY470c-4/view?usp=sharing

Задание на 05.06.2020 г.

Выполните контрольную работу, результаты жду до 18.00. Позже не принимаю!

Задание на 02.06.2020 г.

Решить неравенства №472, №473

Задание на 01.06.2020 г.

Решить неравенства №466, №467

Перейти по ссылке и просмотреть видеоурок

https://youtu.be/7Do2guQwV9E

Задание на 28.05.2020 г.

https://drive.google.com/open?id=1YVf2Oql_uk3SCuicb765JQZvzG8DDTzJ

Задание на 21.05.2020 г.

Задание на 19.05.2020 г.

Задание на 18.05.2020 г.

Задание на 14.05.2020 г.

Выполнить номера №447, №448

Задание на 12.05.2020 г.

Перейдите по ссылке, ознакомьтесь с новой темой, законспектируйте ее и выполните номера №445, №446.

https://drive.google.com/open?id=1-qVGXv4ssustqUd3eQGzZ2kREeWubzN8

Задание на 08.05.2020 г.

Выполнить номера №436, №437

Задание на 07.05.2020 г.

Выполнить номера №430, №431

Задание на 06.05.2020 г.

https://drive.google.com/open?id=1QjAfpfpjJF5j5zoW_bHBO-lnFALWm3Lz

Задание на 30.04.2020 г.

Выполнить номера №424, №425

Задание на 28.04.2020 г.

Выполнить номера №422, №423

Задание на 27.04.2020 г.

Выполнить тесты по теме Иррациональные уравнения.

Такого плана тесты будут у вас на экзамене.

Это для вас как тренажер для подготовки к экзамену
Ответы отправляйте по форме вопрос-ответ( например 1-1)

Задание на 23.04.2020 г.

Задание на 21.04.2020 г.

Выполнить №419, №420

Задание на 20.04.2020 г.

Тему "Иррациональные уравнения" вы можете рассмотреть здесь ↓ (Там же указано домашнее задание)

https://drive.google.com/file/d/1fdXI4EvCni2P0dku3WLvgewEnz3GR_rd/view?usp=sharing

Задание на 16.04.2020 г.

Задание на 14.04.2020 г.

Задание на 13.04.2020 г.

Выполнить №398, №399, №400

Задание на 09.04.2020 г.
Выполнить №392, №393, №394

Задание на 07.04.2020 г.

Используя свойства корней найдите значение числового выражения: № 390, №391

Уважаемые студенты!

С 06.04.2020г. продолжаем работать в режиме дистанционного обучения

Задание на 06.04.2020 г.
Нажмите на ссылку и выполните задание в тетради. Фото с конспектом, таблицей квадратов, формулами и решением отправьте на мою электронную почту
https://drive.google.com/file/d/1ms8q6JoTGddH8uCKpc6WhKUnMNykpJ2F/view?usp=sharing

Задание на 26.03.2020 г.